Номинация «Студенты и аспиранты» |
| |
Гвоздевский Павел Борисович
Санкт-Петербургский государственный университет
(Санкт-Петербург) |
|
Надгруппы subsystem subgroups в исключительных группах: 2A1-доказательство.
В настоящей работе мы докажем ослабленный вариант sandwich classification для надгрупп подсистемной подгруппы E(Δ,R) группы Шевалле G(Φ,R), где Φ - система корней с простыми связями, а Δ - ее достаточно большая подсистема. А именно, мы покажем, что для любой такой надгруппы H существует единственная сеть идеалов σ кольца R, такая что E(Φ,Δ,R,σ) ≤ H ≤ StabG(Φ,R)(L(σ)), где E(Φ,Δ,R,σ) - элементарная подгруппа, связанная с сетью, а L(σ) - соответствующая подалгебра в алгебры Ли Шевалле.
|
| |
Ильин Алексей Игоревич
Высшая школа экономики
(Москва) |
|
О максимальности некоторых коммутативных подалгебр янгианов.
Данная работа посвящена исследованию свойств подалгебр Бете в янгиане Y(gl(n)), где gl(n) - произвольная комплексная простая алгебра Ли. Доказывается, что подалгебры, соответствующие регулярным полупростым элементам, максимальны, более того, являются централизатором своей квадратичной части. Также в работе содержится явное описание квадратичных частей подалгебр Бете, соответствующих регулярным полупростым элементам.
|
| |
Каплун Александр Владимирович
Санкт-Петербургский государственный университет и Санкт-Петербургское отделение Математического института им. В.А.Стеклова
(Санкт-Петербург) |
|
Алгебра эйконалов на метрическом графе.
Алгебра эйконалов – это операторная C*-алгебра, связанная с динамической системой, которая описывает распространение волн в метрическом графе, при этом структура алгебры эйконалов связана с геометрией графа. Целью работы является изучение алгебры эйконалов для случая общего графа. Получено каноничесоке блочное представление алгебры эйконалов, а также описано восстановление данного объекта по спектру соответствующей алгебры.
|
| |
Клемятин Никита Юрьевич
Высшая школа экономики
(Москва) |
|
Когомологии Дольбо комплексных многообразий с действием комплексной группы Ли.
Let G be a complex Lie group acting on a compact complex Hermitian manifold M by holomorphic isometries. We prove that the induced action on the Dolbeault cohomology and on the Bott-Chern cohomology is trivial. We also apply this result to compute the Dolbeault cohomology of Vaisman manifolds.
|
| |
Красненкова Анастасия Владимировна
Московский государственный университет имени М.В. Ломоносова
(Москва) |
|
О формализации модальной логики в системе Coq
В работе исследуются вопросы формализации натурального полимодального исчисления в системе Coq. Построено доказательство корректности указанного исчисления средствами Coq, и проведен детальный анализ данного доказательства. В качестве тестового эпистемического сценария рассматривается известная загадка .грязных детей., показана взаимосвязь данного эпистемического утверждения и критерия полноты для многозначных логик.
|
| |
Логинов Константин Валерьевич
Высшая школа экономики и Независимый Московский университет
(Москва) |
|
Полустабильные вырождения многообразий Фано
Работа посвящена изучению некоторого класса вырождений многообразий Фано. А именно, доказывается, что двойственный комплекс центрального слоя полустабильного семейства Фано является симплексом ограниченной размерности. Это дает подход к классификации таких вырождений: в работе передоказывается классификация в размерности два и доказывается, что в размерностях не выше трех максимальное вырождение единственно и имеет тривиальную монодромию.
|
| |
Осипов Павел Сергеевич
Высшая школа экономики
(Москва) |
|
Проективные гессиановы и сасакиевы многообразия
The Hessian geometry is the real analogue of the Kahler one. Sasakian geometry is an
odd-dimensional counterpart to the Kahler geometry. In the paper, we study the connection
between projective Hessian and Sasakian manifolds analogous to the one between Hessian and
Kahler manifolds. In particular, we construct a Sasakian structure on TM x ℝ from a
projective Hessian structure on M. We are interested in the case of invariant structure on Lie
groups. We define semi-Sasakian Lie groups as a generalization of Sasakian Lie groups. Then
we construct a semi-Sasakian structure on a group G ⋉ ℝn-1 for a projective Hessian Lie group
G. We describe examples of homogeneous Hessian Lie groups and corresponding semi-Sasakian
Lie groups. The big class of projective Hessian Lie groups can be constructed by homogeneous
regular domains in ℝn. The groups SO(2) and SU(2) belong to another kind of examples.
Using them, we construct semi-Sasakian structures on the group of the Euclidean motions of the
real plane and the group of isometries of the complex plane.
|
| |
Сагдеев Арсений Алексеевич
Московский физико-технический институт
(Москва) |
|
О несимметричных диофантовых приближениях
We found new generalizations of classic Hurwitz's theorem on Diophantine approximation and a related result by Robinson. We apply our results to answer Segre's question on asymmetric Diophantine approximation for “almost all" values of asymmetric parameter.
|
| |
Устинов Никита Сергеевич
Санкт-Петербургский государственный университет (Санкт-Петербург) |
|
Эффект кривизны в дробном неравенстве Харди--Соболева со спектральным лапласианом Дирихле
В работе исследуется вопрос о достижимости точной константы в неравенстве Харди-Соболева со спектральным лапласианом Дирихле:
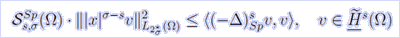
где n ⋝ 2, 0 ∈ δΩ, 0 < σ < s < 1,  . Оказывается, что достижимость точной константы . Оказывается, что достижимость точной константы 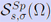 зависит от геометрических свойств области Ω в окрестности начала координат: например, для звездной относительно нуля области константа зависит от геометрических свойств области Ω в окрестности начала координат: например, для звездной относительно нуля области константа 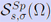 не достигается, тогда как для вогнутой в среднем в нуле области константа не достигается, тогда как для вогнутой в среднем в нуле области константа 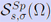 достижима. достижима.
Краткие результаты работы приняты к публикации в [1], полное изложение результатов на английском языке можно найти в препринте [2].
Список литературы:
- Н.С.Устинов. О достижимости точных констант в дробных неравенствах Харди-Соболева со спектральным лапласианом Дирихле. Функц. анализ и его прил., 53:3 (2019).
- N. Ustinov, The effect of curvature in fractional Hardy–Sobolev inequality with the Spectral Dirichlet Laplacian, preprint arXiv:1906.07519 (2019).
|
| |
Фролова Елизавета Дмитриевна
Московский государственный университет имени М.В. Ломоносова (Москва) |
|
Теоремы типа Макаренко-Хухро для алгебр
Предлагаются две теоремы: теорема о больших подпространствах - аналог для алгебр данного Клячко и Милентьевой обобщения теоремы Макаренко-Хухро о больших характеристических подгруппах с тождеством, и теорема - аналог для алгебр Ли и ассоциативных алгебр теоремы Макаренко-Шумяцкого.
|
| |
Номинация «Студенты» |
| |
Алексеев Александр Владимирович
Московский физико-технический институт
(Москва) |
|
Комплекс n-категорий и дифференцирования в групповых алгебрах.
В работе рассматривается бесконечная дискретная группа G и ее групповая алгебра. Строится описание алгебры дериваций групповой алгебры в геометрических терминах ассоциированного с данной группой 2-группоида.
|
| |
Барон Полина Глебовна
Высшая школа экономики
(Москва) |
|
Мера максимальной энтропии для минимальных перекладываний с флипами четырех отрезков.
In this paper, we study the invariant measures for minimal interval exchange transformations with flips. We construct the Rauzy diagram for minimal interval exchange transformations with flips in case of 4 subintervals, exploiting the results obtained in [1]. We introduce the roof function on the parameter space and prove the existence of the measure of maximal entropy for the flow.
References:
- E. Arzhakova, P. Baron. Rauzy Graph and Rauzy Induction for Minimal Interval Exchange Transformations with Flips. Coursework, available at https://bit.ly/2mryxw7 (2017)
|
| |
Дмитриев Михаил Дмитриевич
Высшая школа экономики
(Москва) |
|
Периодические замощения плоскости квадратами.
В работе приводится элементарное доказательство теоремы Кеньёна о том, что периодическое замощение плоскости квадратами с периодами (λ,0) и (0,1) возможно только тогда, когда λ=p±√q2-r2 для некоторых рациональных p≥q≥r≥0. Доказывается аналогичный новый результат об оклеивании прямоугольника квадратами с двух сторон в один слой.
|
| |
Зайцева Юлия Ивановна
Московский государственный университет имени М.В. Ломоносова
(Москва) |
|
Структуры коммутативных алгебраических моноидов на аффинных пространствах.
We study commutative associative polynomial operations An x An → An with unit on the affine space An over an algebraically closed field of characteristic zero. A classification of such operations is obtained up to dimension 3. Several series of operations are constructed in arbitrary dimension.
|
| |
Куликов Алексей Игоревич
Санкт-Петербургский государственный университет
(Санкт-Петербург) |
|
О теореме Хейнса.
В работе изучаются обобщения знаменитой теоремы Хейнса о целых функциях минимального экспоненциального типа с ограниченным минимумом. Показано, что теорема Хейнса верна и в том случае, когда одна функция имеет минимальный тип, а другая конечный, а также что в случае двух функций конечного типа области, где эти функции малы, близки к двум полуплоскостям. Изучен вопрос о том, могут ли эти полуплоскости «закручиваться», и дано точное интегральное условие на возможную скорость вращения этих полуплоскостей.
|
| |
Леонкин Дмитрий Олегович
Высшая школа экономики
(Москва) |
|
Замечательные компактификации PGLn и их кольца Кокса.
В работе «Замечательные компактификации PGLn и их кольца Кокса» изучается вопрос явного (с помощью порождающих и соотношений) задания кольца Кокса для PGLn. С помощью методов выпуклой геометрии получены некоторые общие результаты о порождающих и соотношениях колец Кокса и функциях Гильберта колец Кокса для произвольной размерности и полное описание кольца Кокса для PGL3. Таким образом, нами получено независимое доказательство результата Бриона о порождающих и соотношениях, новые, по всех видимости, результаты о полиномиальности функции Гильберта колец Кокса замечательной компактификации. Также в процессе исследования порождающих в подалгебре кольца Кокса, нами сформулирован и доказан новый, насколько нам известно, результат о кратностях вхождения неприводимых представлений в разложение тензорного произведения фундаментальных представлений SLn.
|
| |
Михеев Иван Евгеньевич
Ижевский государственный университет
(Ижевск) |
|
Задача о диверсификации рубля по двум вкладам в кооперативной постановке.
Рассматривается задача распределения некоторой суммы в рублях на рублевой и другой валютный депозит с целью получения максимального дохода в рублях в конце срока хранения. Предполагается, что лица принимающие решения не знают курса другой валюты в конце срока хранения и ориентируются только на заданные границы возможных изменений. Решение данной задачи зависит от выбора принципа оптимальности. Задача рассматривается в кооперативной постановке. В качестве первичного принципа оптимальности используется принцип гарантированного результата.
|
| |
Морозов Егор Александрович
Высшая школа экономики
(Москва) |
|
Поверхности содержащие две параболы через каждую точку.
We prove (modulo some technical assumptions) that each surface in ℝ3 containing two arcs of parabolas with axes parallel to Oz through each point has a parametrization
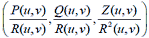 for some P,Q,R,Z ∈ ℝ[u,v] such that P,Q,R have degree at most 1
in u and v, and Z has degree at most 2 in u and v. The proof is based on the observation that
one can consider a parabola with vertical axis as an isotropic circle; this allows us to use
methods of the recent work by R.Krasauskas and M.Skopenkov in which all surfaces containing
two Euclidean circles through each point are classified. Such approach also allows us to find a
similar parametrization for the surfaces in ℝ3 containing two arbitrary isotropic circles through
each point (modulo the same technical assumptions). Finally, we get some results concerning the
top view (the projection along the Oz axis) of the surfaces in question.
for some P,Q,R,Z ∈ ℝ[u,v] such that P,Q,R have degree at most 1
in u and v, and Z has degree at most 2 in u and v. The proof is based on the observation that
one can consider a parabola with vertical axis as an isotropic circle; this allows us to use
methods of the recent work by R.Krasauskas and M.Skopenkov in which all surfaces containing
two Euclidean circles through each point are classified. Such approach also allows us to find a
similar parametrization for the surfaces in ℝ3 containing two arbitrary isotropic circles through
each point (modulo the same technical assumptions). Finally, we get some results concerning the
top view (the projection along the Oz axis) of the surfaces in question.
|
| |
Оганесян Кристина Артаковна
Московский государственный университет имени М.В. Ломоносова
(Москва) |
|
Множества нулей и множества положительности сумм невырожденных синус-рядов с монотонными коэффициентами.
Рассматриваются ненулевые синус-ряды со стремящимися к нулю неотрицательными монотонными коэффициентами. Показано, что множество положительности такого ряда ƒ(x) на отрезке [0, π] имеет меру не меньше, чем π/2 + 0.24, а множество нулей – не больше, чем π/3, причем если значение π/3 достигается, то почти все множество нулей лежит на отрезке [2π/3,π]. Доказано, что для любого n ∈ Ν, отличного от единицы, на интервале (0, 2π/n) выполняется неравенство nƒ(x) > ƒ(nx) всюду, кроме конечного числа точек, в которых обе части равны нулю.
|
| |
Рыбин Дмитрий Алексеевич
Высшая школа экономики
(Москва) |
|
q-характер представлений sln
Generating functions for PBW-grading of irreducible representations of sln of particular type are obtained. Several combinatorial corollaries are proven.
|
| |
Сергунин Андрей Владимирович
Московский физико-технический институт
(Москва) |
|
О количестве точек пересечения прямых и окружностей в ℝ3
В работе изучается структура множеств прямых и окружностей в трехмерном евклидовом пространстве, которые имеют много попарных пересечений. В частности, доказано, что для произвольного множества прямых и окружностей можно либо найти большое число объектов на одной поверхности не более чем второй степени, либо дать нетривиальную оценку на число точек, лежащих на хотя бы одной прямой и хотя бы одной окружности.
|
| |
Спиридонов Игорь Александрович
Высшая школа экономики
(Москва) |
|
Действие автоморфизма графа на пространстве потоков
В работе доказано, что для вершинно 3-связного графа G группа автоморфизмов решетки потоков на этом графе изоморфна прямому произведению группы автоморфизмов графа G на ℤ/2ℤ, а также изоморфна группе симметрий многогранника простых циклов графа G. Доказано, что вершинная 3-связность является необходимым условием для существования первого изоморфизма.
|
| |
Федоров Михаил Сергеевич
Высшая школа экономики
(Москва) |
|
Некоторые особенности распределения вероятностей протекания нескольких жидкостей на шестиугольной решетке
В работе рассматривается равномерная случайная раскраска клеток шестиугольной решетки в 2n-1 цветов (стандартная модель Поттса при бесконечной температуре), которую можно рассматривать как обобщение перколяции на n жидкостей - попарно-независимых, но зависимых в совокупности. В этой модели вводится новая наблюдаемая, которую можно интерпретировать как долю протекающих жидкостей. Для этой наблюдаемой доказывается аналог центральной предельной теоремы и формулируется несколько гипотез на основе численных экспериментов.
|
| |
Черных Георгий Сергеевич
Московский государственный университет имени М.В. Ломоносова
(Москва) |
|
SU-бордизмы: структурные результаты и геометрические представители
В данной работе исследуется теория SU-бордизмов методом спектральной последовательности Адамса-Новикова, следуя работе Новикова 1967 года «Методы алгебраической топологии с точки зрения теории кобордизмов». Восполняются технические детали указанной работы, извлекаются все основные результаты о кольце коэффициентов SU-бордизмов. Исследуется структура естественно возникающих в этом подходе c1-сферических бордизмов W. Приводятся примеры маломерных представителей некоторых специальных классов SU-бордизмов.
|
| |
Чистопольская Алиса Ильинична
Московский государственный университет имени М.В. Ломоносова
(Москва) |
|
Нильпотентные порождающие симплектической алгебры Ли
Let sp2n(𝕂) be the symplectic Lie algebra over an algebraically closed field of characteristic zero. We prove that for any nonzero nilpotent element X in sp2n(𝕂) there exists a nilpotent element Y in sp2n(𝕂) such that X and Y generate sp2n(𝕂).
|
| |